本文作者：刘瑞祥，[遇见数学]感谢刘老师一直来关注支持！

学数学，需要背吗？需要技巧吗？

先说结论：两者都需要。

为什么？

我们经常看到一些人说，数学最重要的是理解概念，死记硬背是要不得的，技巧是不重要的，如此等等。

但是，“死记硬背”要不得，并不代表完全不需要背，概念重要，也不代表技巧不重要。除了小时候要背乘法口诀外，还有一些需要“背一背”的东西。

比如二次方程的求根公式，是由配方法得来的，但是当我们得到这个公式后，再遇到二次方程，往往是直接套用这个公式，而不是从头给方程配方了。这也正是这个公式的意义，它可以让你直接写出答案，不必再配方了。

事实上，所有公式的意义，都是让你不必从头开始一点点推导。原则上说，这些公式都可以直接从概念推出来，但如果你每次用公式都从头推导的话，那这些公式还有什么用呢？

从某个角度来说，公式就像围棋中的定式一样，只要你按照定式走下去，总可以得到一个“不坏”的结果。可为什么前辈围棋大师吴清源先生说自己不背定式（相当于某个数学天才说自己不背公式一样）？因为他是吴清源，是Alpha Go出现之前最接近“围棋之神”的人，他下的棋本身就是定式，我们普通人还是老实一点好。更何况，数学公式的重要性远胜于围棋中的定式。

当然，数学上的公式太多了，人的精力有限，不可能记得所有公式，所以我这里强调的，是背一些重要的公式。这些公式的重要性，基本不亚于乘法口诀。比如 e^x 的导数非常重要，你学会这个之后，自然会计算 a^x 的导数，因为只要你把 a 换成 e^(ln a)，原式子就变成了 e^(x ln a)，用复合函数求导公式就可以算出来了——看，又是公式。

再比如初等数学里，你已经学过了很多三角形面积公式，但是很显然不是全部。比如给出三角形的两个角及其公共边的长度，能不能确定这个三角形的面积？这显然也可以有一个公式，但是一般的书里不会有这个式子，说明这个“公式”不怎么重要。

数学技巧，在某方面和公式差不多：你掌握一些技巧，就容易解决相应的问题。比如传统几何里添加辅助线，就是一种技巧。当然，添加辅助线的方法很多，很难全部掌握，我们只要记一些常见的思路就可以了。

再比如，我前些天看到这样一道题：已知 a, b, c 均不为 0，且 a+b+c=0，求

感觉有难度是不是？

其实这是一道选择题，而且四个备选答案都是不含字母的纯数值。这就启示我们，无论 a, b, c 到底是什么值（当然得符合条件），以上表达式的值都不变。显然，我们只要设一下这三个变量的值就可以了：比如可以令 a=1, b=1, c=-2，带入原式即得到结果。这就是做选择题的特殊值法——这当然是一种解题技巧。

如果你想要得到一个“严谨”的答案，那就费了劲了：

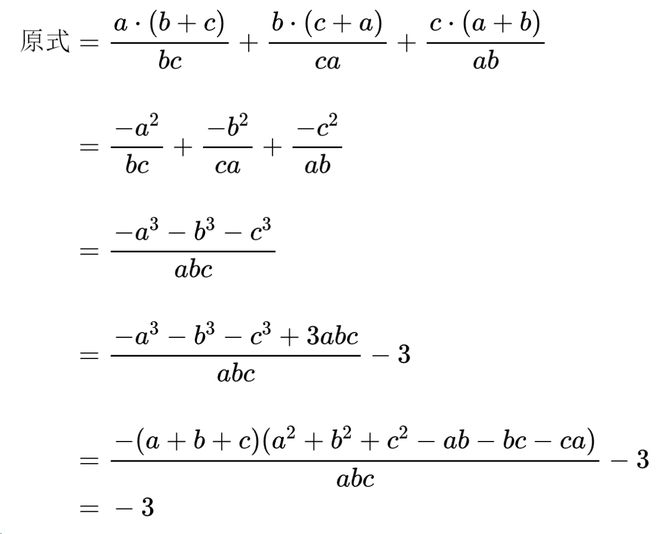
这样一来，严谨是严谨了，多麻烦。

数学上的技巧往往和定理、公式、法则等等密切相关。

笔者以前的文章里，曾经提到如果给出平面坐标系三个点的坐标(x₁, y₁), (x₂,y₂), (x₃,y₃)，则过此三点的圆方程为

曾有网友说看不出来这个行列式为什么满足题意。如果这些网友不是没学过行列式，那就是太疏于行列式的性质了。

首先，如果将 (x₁, y₁), (x₂,y₂), (x₃,y₃) 这三个坐标的任意一个带入以上方程，都可以得到两个相同的行，因为行列式如果两行相同（或对应成比例），则行列式的值为 0，所以这三个点的坐标都满足以上方程。

又因为，如果将行列式按第一行展开，则二次项只有 (x²+y²)，即 x² 和 y² 的系数相同，没有 xy 项，这正是圆方程的特征(该行列式按第一行展开的结果如下)。

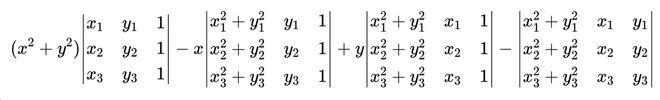
所以，行列式变形的技巧是多么重要，当然其它技巧亦然。我觉得，完全鄙视技巧的人，要么是“数学之神”，要么就是不屑于解决具体问题、只会高谈阔论的人。当然，我这么说，也不是要把解题技巧吹上天，而是提倡正确看待解题技巧——这东西固然不能“包治百病”，但完全没有也不行。